Diffie-Hellman Key-Agreement

(Copied/paraphrased/annotated from the script on Discrete Mathematics HS21 by Prof. Ueli Maurer)

Introduction and Motivation

Until the 1970’s, number theory was considered one of the purest of all mathematical disciplines in the sense of being furthest away from any useful applications. However, this has changed dramatically in the 1970’s when crucial applications of number theory in cryptography were discovered. In a seminal 1976 paper (W. Diffie and M.E. Hellman, New directions in cryptography, IEEE Transactions on Information Theory, vol. 22, no. 6, pp. 644-654, 1976), Diffie and Hellman proposed the revolutionary concept of public-key cryptography. Most security protocols, and essentially all those used on the Internet, are based on public-key cryptography. Without this amazing and paradoxical invention, security on the Internet would be unthinkable.

Consider the key distribution problem. In order to encrypt the communication between two parties, say Alice and Bob, they need a secret key known only to them. How can they obtain such a key in a setting, like the Internet, where they initially share no secret information and where they are connected only by an insecure communication channel to which a potential adversary has access? We describe the famous Diffie-Hellman protocol which allows to solve this seemingly paradoxical problem.

The Diffie-Hellman Protocol

📎 Let $f (x_{1}, \dots, x_{k})$ be a multi-variate polynomial in $k$ variables with integer coefficients, and let $m \geq 1$ . Then

$R_{m} (f (a_{1}, \dots, a_{k})) = R_{m} (f (R_{m} (a_{1}), \dots, R_{m} (a_{k}))) .$

The Diffie-Hellman protocol, as originally proposed, makes use of exponentiation modulo a large prime $p$ , for instance with 2048 bits. While $y = R_{p} (g^{x})$ can be computed efficiently using the above corollary of modular arithmetic, even if $p$ , $g$ and $x$ are numbers of several hundred or thousands of digits, computing $x$ when given $p$ , $g$ and $y$ is generally (believed to be) computationally infeasible. This problem is known as (a version of) the discrete logarithm problem. The security of the Diffie-Hellman protocol is based on this asymmetry in computational difficulty. Such a function, like $x ⟼ R_{p} (g^{x})$ , is called a one-way function: it is easy to compute in one direction but computationally very hard to invert.

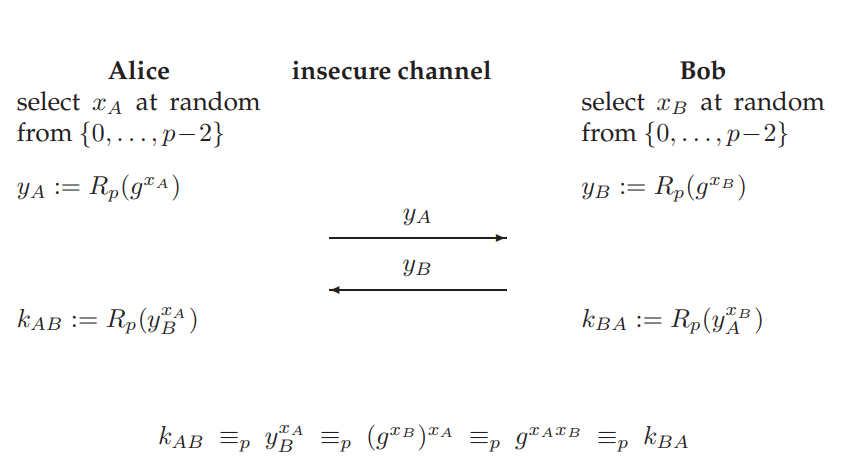
Untitled

The prime $p$ and the basis $g$ (e.g. $g = 2$ ) are public parameters, possibly generated once and for all users of the system. The protocol is symmetric, i.e., Alice and Bob perform the same operations. The exchange of the so-called public keys $y_{A}$ and $y_{B}$ must be authenticated, but not secret. It is easy to see that Alice and Bob end up with the same value $k_{A B} = k_{B A}$ which they can use as a secret key for encrypting subsequent communication. In order to compute $k_{A B}$ from $y_{A}$ and $y_{B}$ , an adversary would have to compute either $x_{A}$ or $x_{B}$ , which is believed to be infeasible.

Diffie-Hellman for General Groups

Diffie-Hellman Key-Agreement for General Groups